В каком классе изучают синусы и косинусы, Программа по математике (9 класс)

Математика, 9 класс. Зачем нужны косинусы? В начальных классах начальной школы ученики знакомятся с основными понятиями тригонометрии, такими как угол, сторона, прямоугольный треугольник. И как мы узнаем позже, синус и косинус всегда больше минус единицы. Search for:.
Чтобы указать значения тангенса и котангенса тех же углов достаточно вспомнить ОТТ, т. Но запоминать эти формулы не обязательно. Для преобразования таких выражений достаточно знать знаки тригонометрических функций по четвертям и еще одну притчу. А лошадь кивала головой по той оси, на которой располагался угол являющиеся границами первой и третьей четвертей соответственно, лежат на оси Оу, то лошадь кивком головы подтверждала смену функции на конфункцию.
А для углов наоборот отрицала. Математику оставалось лишь записывать ответ, указывая знак данной функции. Формулы сложения — это та, группа формул которую нужно знать наизусть. Но для их запоминания можно тоже воспользоваться ассоциативным приемом. У косинуса функции одноименные, а у синуса разноименные.
Так и у наших функций, если функции идут одноименные, то знаки не совпадают, а если разноименные, то совпадают. Если сложить косинус разности с косинусом суммы двух углов,то мы получим формулу суммы косинусов:. В качестве домашнего задания ребятам можно предложить, используя рассмотренные на уроке приемы, записать тригонометрические формулы.
И сделать это нужно несколько раз. Урок алгебры в 9-м классе по теме "Тригонометрические формулы и приемы их запоминания" Слаткова Оксана Михайловна. Назад Вперёд.
Цель урока: познакомить учащихся с мнемоническими правилами для запоминания формул приведения и значений тригонометрических функций некоторых углов; способствовать развитию логического мышления и устной математической речи при поиске решения поставленной проблемы; воспитывать внимательность, наблюдательность и самостоятельность Замечание: при проведении этого урока использовалась интерактивная доска и пульты дистанционного тестирования Activote, но провести его можно без этого оборудования, при помощи прилагаемой презентации.
Ход урока I. Изучение нового материала знакомство с приемами запоминания тригонометрических формул. Табличные значения тригонометрических функций. Формулы сложения. Инструктаж домашнего задания.
Итог урока интерактивное тестирование. Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона — это гипотенуза. И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:.
Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:. А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество :. Рекомендую потренироваться и сделать это самим. Для удобства соберем все формулы вместе.
Но для начала и для 9-го класса этого вполне достаточно. Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу 1 : зная, например, чему равен косинус, можно легко найти синус, и наоборот. Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа. Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы.
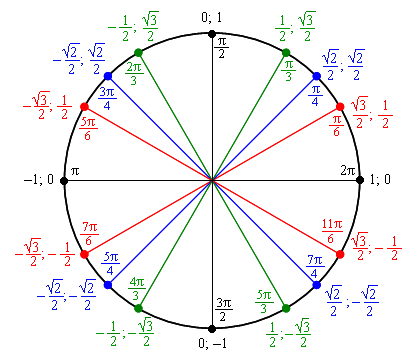
Рассмотрим еще пример:. Все тригонометрические функции берутся от некоторых углов. Если нам известен угол, то это значит, что нам известно и значение тригонометрической функции. При помощи калькулятора можно посчитать значение тригонометрической функции от любого угла за редкими исключениями, поговорим об этом позже. Но есть, так называемые, стандартные углы, значения от которых всеобще известны. В школе пользоваться калькулятором нельзя, поэтому подавляющее большинство заданий из тригонометрии будет связано именно с этими углами, особенно в 9-м классе.
Обычно стандартные углы записываются при помощи таблицы, которую придется выучить:. Наблюдательный читатель мог обратить внимание, что значения всех тригонометрических функций в таблице 1 либо положительны, либо равны нулю. Отрицательных значений нет совсем. Дело в том, что в таблице 1 рассмотрены далеко не все стандартные углы, а только до 90 градусов. Есть расширенная версия этой таблицы, где указано больше стандартных углов.
И у некоторых тригонометрических функций значения будут отрицательны. Пример такой таблицы:. В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости.
В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы. Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых. Ну что ж, да, тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно.
Просто пока запомните выводы, которые мы сделали в предыдущем абзаце. Рассмотрим пример на тригонометрию, по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:. По определению синус в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга.
Некоторые даже будут из реального ЕГЭ:. Задание из ЕГЭ по профильной математике.

У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Опять обратимся к нашим формулам и пытаемся найти такую, в которой есть и синус, и тангенс.
И тут оказывается, что такой формулы нет. Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул можно найти три оставшихся, именно для этого формулы и нужны. Во многих задачах по геометрии часто удобно использовать тригонометрию для нахождения углов или сторон треугольника. Даже одни из самых мощных теорем в курсе школьной геометрии называются теорема косинусов и теорема синусов. Это нам как бы намекает на тесную связь этих двух разделов математики. И определение тригонометрических функций в 9-м классе дается через геометрическую фигуру - прямоугольный треугольник.

Не пугайтесь, все нам не понадобится. Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии. Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных.
А значит в них выполняются все соотношения для тригонометрических функций. А значит можно записать формулы, следующие из определения тригонометрических функций:.