Почему планеты движутся по эллипсу

Artem Новичок Сообщений: 26 Благодарностей: 2. В перигелии скорость планеты наибольшая, в афелии —наименьшая. Kepler в нач. Просто мне самому интересно стало.
В одно и то же время радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную. Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит. Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и средним расстоянием от Солнца до планеты или спутника устанавливается связь.
Меня не интересует всё это для Солнечной системы. Андрей О. КФМН физика тведого тела , сейчас пенсионер-инженер.
У Кеплера все орбиты- эллипсы. Он, из философских соображений, предпочел бы окружности, но не получилось. Все три закона описывают свойства элиптических орбит. Поэтому даже в обобщённый третий закон входят полуоси. Вывод креативной формулы определения скорости планеты про орбите по одному параметру только по удалению от центра гравитации.
Вычислим куб большой полуоси орбиты и квадрат периода обращения планеты вокруг Солнца для всех планет. Найдем погрешность отклонения этих величин. И тогда возможно увидеть в Астрономической Системе Отсчета, что: Кубы радиусов орбит и квадраты периодов обращения планет равны. Чем ни дальше находится планета от центра гравитации, тем её скорость меньше.
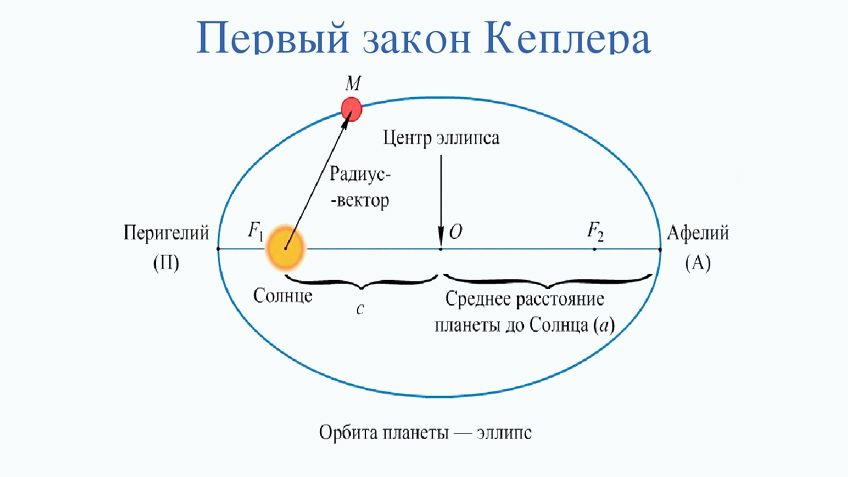
И чем ни ближе находится планета к центру гравитации, тем скорость её больше. Данная формула позволяет сделать вывод, что скорость планеты на орбите зависит от свойства пространства. В точке F1 см. В фокусе орбиты находится светило Солнце. Величину дуги A2B2 в афелии можно вычислить как произведение скорости планеты v2 на малый отрезок времени t. Для д-о-с-т-а-т-о-ч-н-о м-а-л-о-г-о времени площадь,заметаемая радиусом - вектором R2 в афелии, можно представить как площадь треугольника А2B2F1.
Учитывая, что вектор скорости V2 в афелии перпендикулярен радиусу-вектору R2 , то малый треугольник F1А2B2 — прямоугольный. Но радиус — вектор в афелии больше, чем радиус-вектор в перигелии и следовательно площади не равны.
Площадь заметаемая радиусом — вектором орбиты , за одно и тоже время , в афелии больше чем площадь заметаемая радиусом — вектором в перигелии. Первая ошибка великого немецкого астронома и мыслителя Иоганна Кеплера заключалась в том, что что убывание силы тяготения он рассматривал только в первой степени: «силы тяготения действуют не в трёхмерном пространстве, а лишь в плоскости планетных орбит и значит, и сила притяжения должна изменяться пропорционально не квадрату расстояния, а первой степени».
Вторая ошибка великого немецкого астронома и мыслителя Иоганна Кеплера заключается в том, что второй закон Кеплера является верным только в том случае, когда эксцентриситет орбиты планеты равен нулю и планеты движутся по окружности, а не по эллипсу. А в том случае, когда планета движется по эллипсу закон площадей, заметаемых радиусом — вектором планеты отличается от второго закона, высказанного Иоганном Кеплером и математически принимает другой вид. В других точках орбиты закон площадей имеет сходное выражение.
Этот закон заметания площадей является универсальным и подходит для эллиптических орбит. А если радиусы — векторы совпадают и планета движется по окружности, то заметаются равные площади за одно и то же время, и выполняется второй закон Кеплера.

Обобщенный Новый Закон заметания площадей включает в себя второй закон Кеплера как частный случай. Выведенный закон заметания площадей радиусами — векторами планет характеризует реальную существующую зависимость, связанную с метрикой пространства под действием гравитационного поля.
Гравитационное поле придаёт определенные свойства параметрам системы в зависимости от массы системы, что будет показано позднее. Тело движется по параболической траектории.
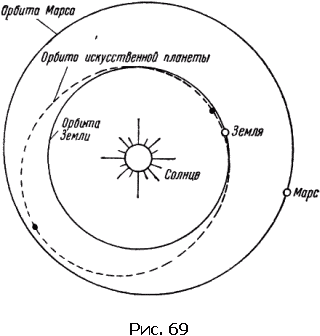
Тело удаляется на бесконечность, имея запас кинетической энергии. Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля. Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли. Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца искусственная планета.
При этом корабль будет удаляться от Земли по параболической траектории. Мы проиллюстрировали понятие первой и второй космической скорости рисунком. При начальной скорости v 2 корабль будет двигаться по параболе, а при еще большей начальной скорости — по гиперболе.
Космические скорости. Указаны скорости вблизи поверхности Земли. Дистанционный экзамен. Две работы по задний. Знайти початкову довжину дроту якщо деформуюча сила створена тягарем масою кг абсолютное видовження мм товщина дроту мм модуль Юнга ГПа. Физика электронных приборов. Решить задачу Равноускоренное прямолинейное движение.

Справочник Онлайн-калькуляторы Тесты с ответами. Как работает сервис. Первый закон Кеплера Определение 1 Планеты Солнечной системы движутся по эллиптическим орбитам. Радиус-вектор планеты описывает в равные промежутки времени равные площади. Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит. Всё ещё сложно? Все услуги.
Предыдущая статья Третий закон Ньютона Следующая статья Вращение твердого тела. Выполненные работы по физике. Дистанционный экзамен Вид работы: Онлайн-помощь Выполнена: 5 января г. Стоимость: 2 руб Заказать такую же работу.